Hornady Guide to External Ballistics

Hornady provides a good, basic Guide to External Ballistics, covering the key principles of small arms ballistics. This is a good starting point to learn how bullet shape, wind, and velocity determine how bullets perform in flight.

If you’ve ever wondered about the meaning of Ballistics Coefficient, or wondered how different zeros affect bullet trajectories, this article will explain the basics that you need to know. Here’s an example:
Ballistic Coefficient Definition
“A ballistic coefficient is the measure of a bullet’s relative ability to overcome air resistance. Each bullet can be assigned a numerical value expressing this efficiency. The basis of this value is a ratio comparing the performance characteristics of a particular bullet against the known trajectory characteristics of a standard projectile. The ratio compares the drag of a bullet (loss of velocity caused by air resistance encountered in flight) to the drag of the standard projectile. Expressed as a formula:

The standard projectile on which all Hornady Bullets were compared was the G1 Model, based on work begun in France and refined at the U. S. Army Ballistic Research Laboratories, Aberdeen Proving Ground, Maryland. Ballistic coefficients for all Hornady Bullets were determined by computer calculations using data from test firing research performed in our 200 yard underground test range.”
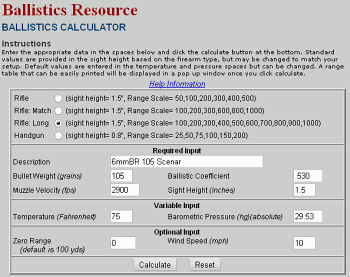
Hornady also offers a free, interactive Ballistics calculator on its web site. While not as detailed or sophisticated as the JBM web ballistics calculator, the Hornady Ballistics Calculator is clean, simple, and easy to use. This will generate bullet drop in minutes of angle (MOA) at distances out to 1000 yards, along with wind drift in MOA and inches. The Hornady ballistics calculator also allow you to pre-select for handgun, short-range rifle, match (High Power) rifle, and long-range rifle. This simplifies the data presented, giving you just the ranges you need.
CLICK HERE for Hornady Ballistics Calculator



















If I sight my rifle (.308/22 inch barrel using 150 grain commercial bullets) to hit 1/2 inch above bulls eye at 50 yards, where will it hit( for hunting purposes only) at: 100, 200, & 300 yards?
Thanks, previously sent with site instead of sight.
If I fire a 7.62 mm round from a sniper rifle with a muzzel velocity of 792.48 m/s, at what angle would I need to hold the rifle in order to achieve a range of 3320 meters. Taking into account air resistance. I can figure this without taking air resistance into account. Any help?
Can you describe how BC is used in an equation for drag, as in
F_drag = C v^2
where C is a constant (involving BC in some way) and v = velocity?